INTEGRAL SUBTITUSI
Pengertian Integral Subtitusi
atau ialah salah satu metode untuk mencari suatu integral dengan mensubstitusi salah satu variabel dan mengubahnya menjadi sebuah bentuk yang lebih sederhana.
Integral dengan teknik/metode substitusi digunakan ketika proses pengintegralan tidak bisa diselesaikan dengan rumus-rumus dasar integral, atau seandainya bisa diselesaikan namun akan memerlukan proses yang cukup panjang.
Rumus Dasar
- Konstanta
∫ k dx = kx + c·
- xn dg. n ≠ -1
∫ xndx = 1/n+1 . xn+1 + c
- Khusus x-1
∫ 1/x dx = ℓn IxI + c
Dalam pengintegralan dengan metode substitusi, tentunya kita harus sudah menguasai konsep-
konsep turunan, dimana adalah turunan u terhadap x..
Misalkan u = 2x + 1, turunan u terhadap x ditulis :
Misalkan u = 2x + 1, turunan u terhadap x ditulis :
= 2 ⇔ du = 2 dx
Contoh Soal dan Pembahasannya
2. ∫ x2 (x3 + 5)7 dx =
Pembahasannya :
Misalkan : u = x3 + 5
= 3x2 ⇔ = x2 dx
·


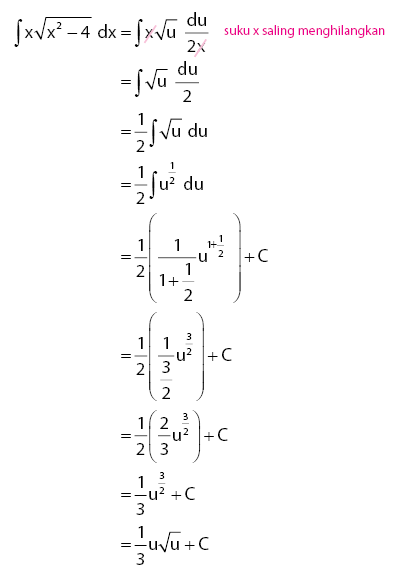
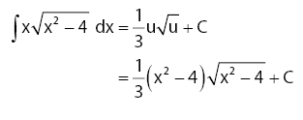


Komentar
Posting Komentar