Integral Subtitusi Trigonometri Tan & Sin

Teknik Integral: Substitusi Trigonometri Tan & Sin

Teknik integral subtitusi trigonometri dapat digunakan untuk menyelesaikan integral yang memiliki bentuk akar, sehingga dapat menghilangkan akar tersebut dalam integran. Kita dapat melakukannya dengan identitas phytagoras

by Yosep Dwi Kristanto

Contoh 1: Substitusi Trigonometri

Selesaikan,

Pembahasan Untuk menggunakan substitusi trigonometri, kita harus melihat bahwa 

√(9 – x²) merupakan bentuk dari √(a² – u²). Sehingga kita dapat menggunakan substitusi

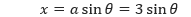
Sehingga, persamaan yang menghubungkan variable x dan θ di atas dapat dimodelkan ke dalam segitiga siku-siku sebagai berikut.

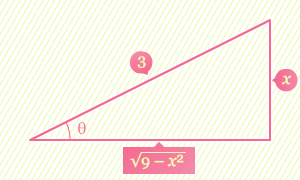
Dengan menggunakan turunan dan segitiga di atas, kita mendapatkan

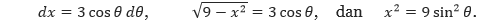
Sehingga, dengan menggunakan substitusi dihasilkan

 

Perhatikan bahwa segitiga pada gambar di pembahasan Contoh 1 tersebut, dapat juga digunakan untuk mengubah θ kembali menjadi x sebagai berikut.

Contoh 2 : Substitusi Trigonometri

Gunakan substitusi trigonometri untuk meniadakan notasi akar pada bentuk $\sqrt{4-9x^2}$.

Pembahasan : 

Ekspresi $4-9x^2$ identik dengan identitas Pythagoras:

$1-{\sin }^2\theta ={\cos }^2\theta$

Substitusi $x$ sebagai sinus bisa menjadi solusi.
Sekarang, untuk mendapatkan koefisien yang sama pada bentuk trigonometri, kita harus mengubah koefisien $9$ pada ekspresi $4-9x^2$ menjadi $4$ (supaya bisa difaktorkan).
Untuk itu, kita dapat memisalkan

$x=\frac{2}{3}\sin \theta$

sehingga diperoleh

$\begin{array}{cc}\sqrt{4-9x^2}& =\sqrt{4-9{\left(\frac{2}{3}\sin \theta \right)}^2}\\ & =\sqrt{4-9\left(\frac{4}{9}{\sin }^2\theta \right)}\\ & =\sqrt{4-4{\sin }^2\theta }\\ & =\sqrt{4(1-{\sin }^2\theta }\\ & =\sqrt{4}\cdot \sqrt{{\cos }^2\theta }\\ & =2|\cos \theta |\end{array}$
Karena kita tidak dapat mengestimasi nilai $\theta$, maka notasi nilai mutlak tidak dapat dihilangkan pada bentuk $|\cos \theta |$.

Contoh 3: Substitusi Trigonometri: u = a tan θ

Tentukan,

Pembahasan Misalkan u = 2x, a = 1, dan 2x = tan θ, seperti yang dapat digambarkan sebagai berikut.

Sehingga, kita mendapatkan

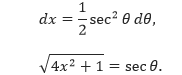
Dengan menggunakan substitusi trigonometri, didapatkan

Selanjutnya kita dapat memperluas penggunaan dari substitusi trigonometri untuk menyelesaikan integral yang memuat bentuk (a² – u²)n/2 dengan menuliskan bentuk tersebut ke dalam